Odległości od płaszczyzny
| Odległości od płaszczyzny | |
|---|---|
| Kategorie | Moduły obliczeniowe |
| Rozszerzenie dla pliku | .oop |
| Ścieżka w programie | Obliczenia -> Odległości od płaszczyzny |
| Powiązania | Tachimetria |
Moduł Transformacja 3D jest przeznaczony dla potrzeb takich zagadnień jak transformacja współrzędnych przestrzennych między różnymi układami odniesienia, przeliczenia współrzędnych zrealizowanej konstrukcji do układu teoretycznego, czy też w obliczeniach przemieszczeń obiektów przestrzennych.
Obliczenia można zrealizować z wykorzystaniem 8 modeli: translacja, przekształcenie izometryczne (przesunięcie i obrót bez zmiany skali), transformacja Helmerta (przesunięcie, obrót i jednakowa zmiana skali dla wszystkich osi układu), przekształcenie przez podobieństwo (przesunięcie, obrót i zmiana skali dla każdej osi inna) wraz z różnymi kombinacjami równej skali (np. sX=sY, sX=sZ, sX=sY=sZ), a także pełna transformacja afiniczna zawierająca oprócz przesunięcia, obrotu i zmiany skali również tzw. skoszenie. Wybór właściwego modelu uzależniony jest od konkretnego zadania. Transformacja izometryczna może być wykorzystywana np. w pomiarach kontrolnych zrealizowanej konstrukcji stalowej i wyznaczeniu odchyłek od kształtu teoretycznego, a także przy przechodzeniu z układów pomiarowych do układu projektowanego konstrukcji (np. statku). Model transformacji Helmerta będzie wykorzystany wtedy gdy układ pierwotny i wtórny cechuje się innym parametrem skali, np. gdy oba pomiary były zrealizowane różnymi instrumentami. W przypadku badania deformacji obiektu będzie przydatna transformacja afiniczna, gdyż podczas realizacji obliczeń program wyznacza wprost parametry kątów obrotu i zmiany skali względem każdej osi układu współrzędnych, a także wyznacza skoszenia kształtu.
W pakiecie otrzymuje się również :
Odległości od płaszczyzny - moduł ten pozwala na przeliczenie współrzędnych XYZ mierzonego obiektu z układu pomiarowego na układ projektowy. Transformacja zachowuje skalę długości, natomiast dokonuje obrotu i przesunięcia w przestrzeni 3D.
Danymi są współrzędne XYZ pozyskane w dowolny sposób, np.:
- obliczone na podstawie danych obserwacyjnych w module Tachimetria i zapisane do tabeli roboczej,
- wprowadzone bezpośrednio do roboczej tabeli współrzędnych programu,
Współrzędne te należy zaznaczyć w tabeli współrzędnych i poprzez funkcję Kopiuj/Wklej wkleić do modułu Transformacja Przestrzenna. Następnie należy uzupełnić dane punktów wartościami — W wz., H wz., G wz. (szerokość, wysokość i głębokość). Są to wymiary występujące w projektach przekrojów. Wartości te można także zapisać w tabeli współrzędnych (lub je tam zaimportować, np. z pliku tekstowego), a następnie przez wprowadzanie numerów punktów w module, wprowadzać jako dane. Po ich wprowadzeniu, należy zaznaczyć trzy punkty jako bazowe (krzyżyk przy numerze punktu), wyznaczające płaszczyznę względem której będzie obliczana transformacja pozostałych punktów.
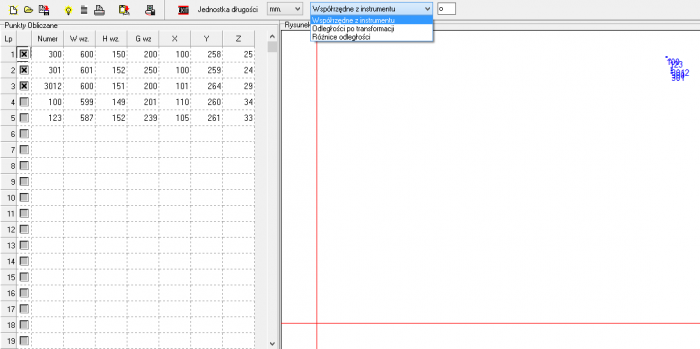
Po wykonaniu obliczeń, wyniki są widoczne po wybraniu w okienku rodzaju danych:
- Współrzędne (z instrumentu),
- Odległości po transformacji — wartości W, H, G po transformacji,
- Różnice odległości — w tym wypadku są podane odchyłki pomiędzy wartościami wzorcowymi a wartościami po transformacji,
Dane i wyniki można przeglądać w jednostkach:
- m- metry,
- dm- decymetry,
- cm- centymetry,
- mm - milimetry,
- km - kilometry,
Po obliczeniach widoczny jest także podgląd graficzny przetransformowanych punktów
Oś pionowa rysunku to oś H, oś pozioma W.
Moduł ten ma zastosowanie np. przy pomiarach elementów kadłubów okrętowych lub innych wielkogabarytowych obiektów (nadwozia autobusów, lokomotyw), które należy skontrolować, aby uzyskać informację, czy zostały wykonane zgodnie z projektem.
Transformowane są wszystkie współrzędne punktów obiektu (XYZ) jednocześnie i jest możliwość wyznaczenia odchyłek od wymiarów teoretycznych, przy założeniu bezbłędnych trzech punktów obiektu. Dla szybkiego uzyskania współrzędnych do obliczeń przydatne są tachimetry bezlustrowe o dużej dokładności pomiaru odległości i kątów. Ponadto, jeżeli zachodzi konieczność pomiaru obiektu z kilku stanowisk, można to zrobić, wykorzystując konstrukcje typu wcięcie wstecz itp., aby uzyskać współrzędne punktów w jednym układzie współrzędnych.