Ciąg poligonowy
| Ciąg poligonowy | |
|---|---|
| Kategorie | Moduły obliczeniowe |
| Rozszerzenie dla pliku | .plg |
| Ścieżka w programie | Obliczenia ->Ciąg poligonowy |
Ciąg poligonowy - moduł obliczania współrzędnych punktów pomierzonych w ciągu poligonowym (otwartym, zamkniętym, wiszącym). Pozwala na określenie współrzędnych ale nie jest to metoda z wyrównaniem ścisłym ! Do tego używamy modułu Wyrównanie ścisłe pamiętając równocześnie, że umiarowy, typowy ciąg poligonowy nie bardzo nadaje się do wyrównania, warto środkowe punkty ciągu wzmocnić dodatkowymi obserwacjami.
Dane wprowadza się w dwóch tabelkach. W górnej wprowadza się dane punktów nawiązania. W zależności od posiadanych danych nawiązania można wprowadzać dwa punkty wyznaczające bok nawiązania lub jeden punkt i azymut. Dane nawiązania wprowadza się zgodnie z oznaczeniami przedstawionymi na rysunku obok tabelki.
Ciąg poligonowy a zadanie tachimetryczne
Przycisk ten pozwala na generowanie ciągów poligonowych na podstawie obserwacji w stanowiskach tachimetrycznych. Podczas pomiaru tachimetrii należy rejestrować obok pikiet również kolejne punkty ciągu poligonowego, oznaczając je jako nawiązania. Należy pamiętać, aby na
wszystkich stanowiskach (oprócz pierwszego i ostatniego stanowiska) były mierzone dwa nawiązania (na poprzedni i następny punkt ciągu).
Punkty ciągu mogą być mierzone w dwóch położeniach lunety, wówczas trzeba podać taki sam numer punktu dla pomiarów w obu położeniach lunety. Po transmisji stanowisk tachimetrycznych do C-Geo , opisywana funkcja umożliwia stworzenie ciągu poligonowego, składającego się z maksymalnie 1000 stanowisk. Jeżeli w aktualnym projekcie znajdować się będą stanowiska tachimetryczne pojawi się tabela, która ułatwi wybór numeru punktu początkowego ciągu, a następnie wybór kolejnych punktów ciągu spośród dostępnych punktów nawiązań tachimetrycznych.
przycisk daje możliwość eksportu danych z ciągów zawartych w projekcie do postaci akceptowalnej przez program do wyrównania sieci prof. E.Osady.
Przykład obliczenia:
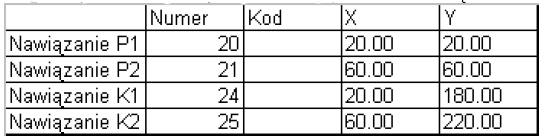
Ciąg poligonowy otwarty tworzy sześć punktów. W górnej tabelce podajemy numery punktów nawiązania:
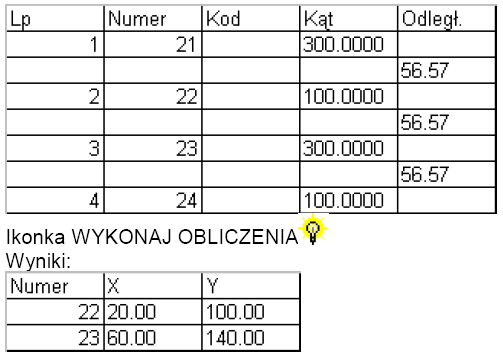
W dolnej tabelce wpisujemy: